Energy-Based Models for Grasp Planning

Abstract

State-of-the-art grasp planning techniques typically use a two-stage approach: a grasp generator network proposes candidate grasps, and a grasp evaluator network estimates the probability of success. However, these two stages act independently — no backpropagation occurs between them. This disjointed structure limits performance and consistency.

This project explores how energy-based models (EBMs) can unify grasp generation, evaluation, and refinement within a single differentiable framework. Given a scene, a grasp can be generated, evaluated, and refined in one shot by descending along the energy manifold. Trained contrastively on ~200,000 examples from DexNet 2.0 using a noise-contrastive estimation (NCE) loss, the model learns to assign low energy to successful grasps and high energy to unsuccessful ones.

Results suggest the EBM generalizes to novel scenes, differentiates good from bad grasps, and produces viable grasp candidates — all within a single integrated system.

Motivation

Grasping is one of the core unsolved problems in robotics. Despite progress from deep learning, grasp planning techniques often rely on disjoint modules for sampling and evaluation. These separate modules prevent gradient flow and limit adaptability.

By contrast, energy-based models represent grasp quality as a continuous energy landscape, where high-quality grasps correspond to low-energy regions. This formulation enables optimization-based refinement — grasp candidates can be iteratively improved by descending the energy manifold toward local minima.

This work demonstrates how EBMs can unify the grasping pipeline — generating, evaluating, and refining grasps in a fully differentiable loop.

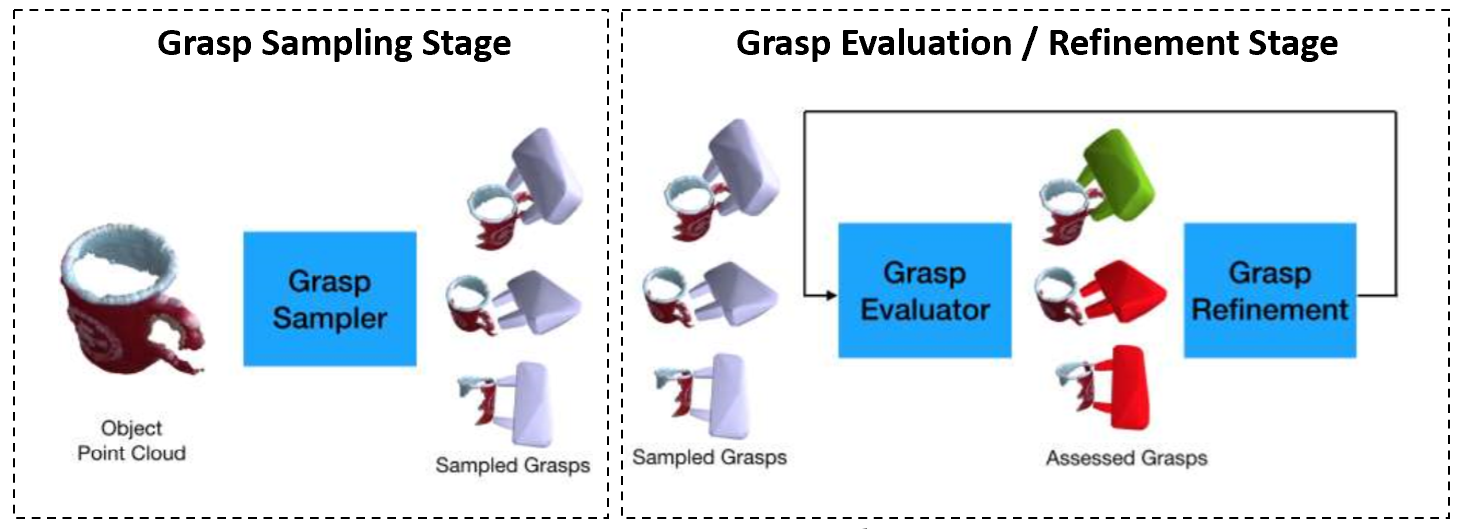
two-stage-approach — Figure 1: The traditional two-stage grasp planning approach, in which grasp sampling and evaluation are separate (image adapted from Mousavian et al. [2]).

Method

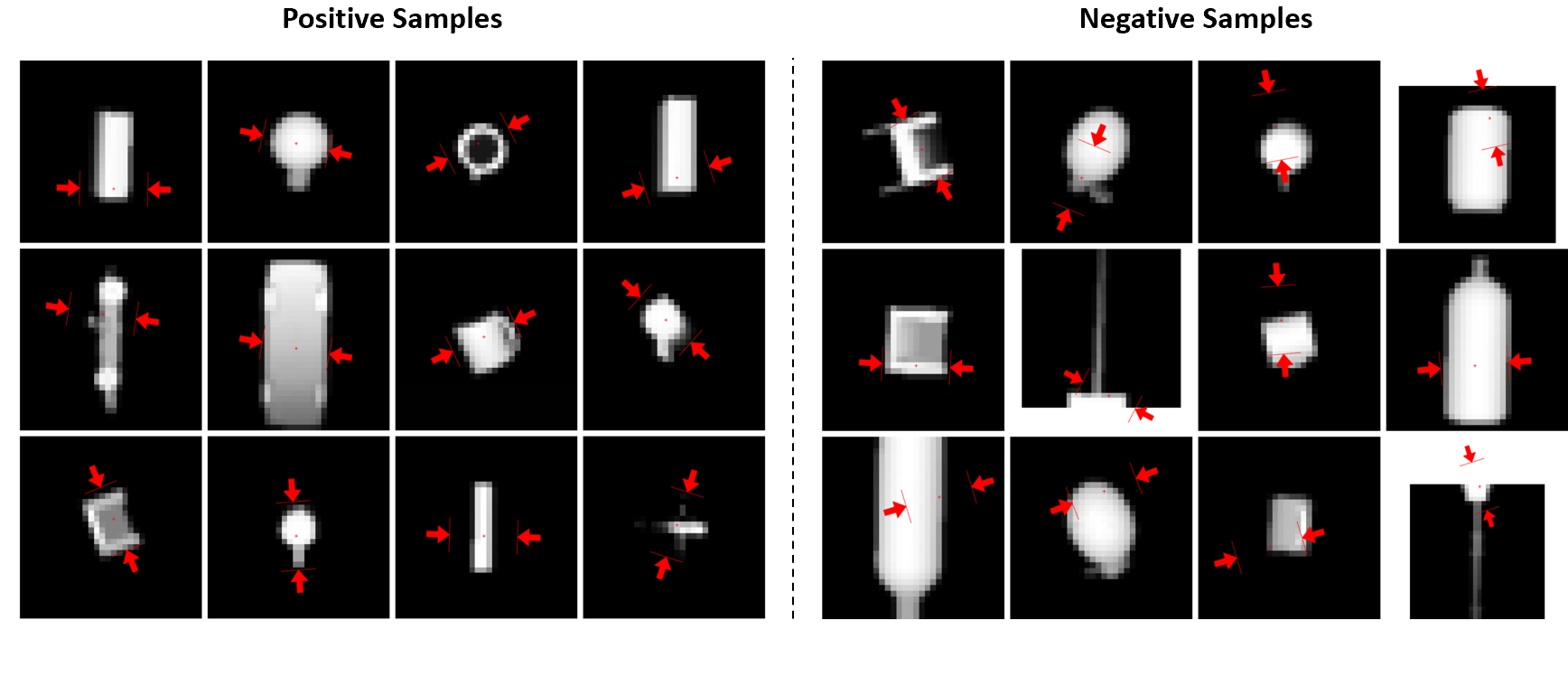
An energy-based model defines a scalar energy (E(x, y)) over depth image (x) and grasp configuration (y). Positive samples (successful grasps) are assigned low energy, while negative samples (failed grasps) are assigned high energy.

During inference, grasps are initialized randomly and refined by gradient descent on (E(x, y)), yielding improved candidates that converge to local minima on the manifold. The NCE loss is used for training:

\[L = \frac{1}{n^+} \sum\_{i=1}^{n^+} \ell_i\] \[\ell*i = \frac{E_w(x_i, y_i)}{\tau} + \log \left[ \exp\left(\frac{-E_w(x_i, y_i)}{\tau}\right) + \sum*{j=1}^{n^-} \exp\left(\frac{-E_w(x_j, \hat{y}\_j)}{\tau}\right) \right]\]

where (\tau) is a temperature hyperparameter controlling the sharpness of the energy separation.

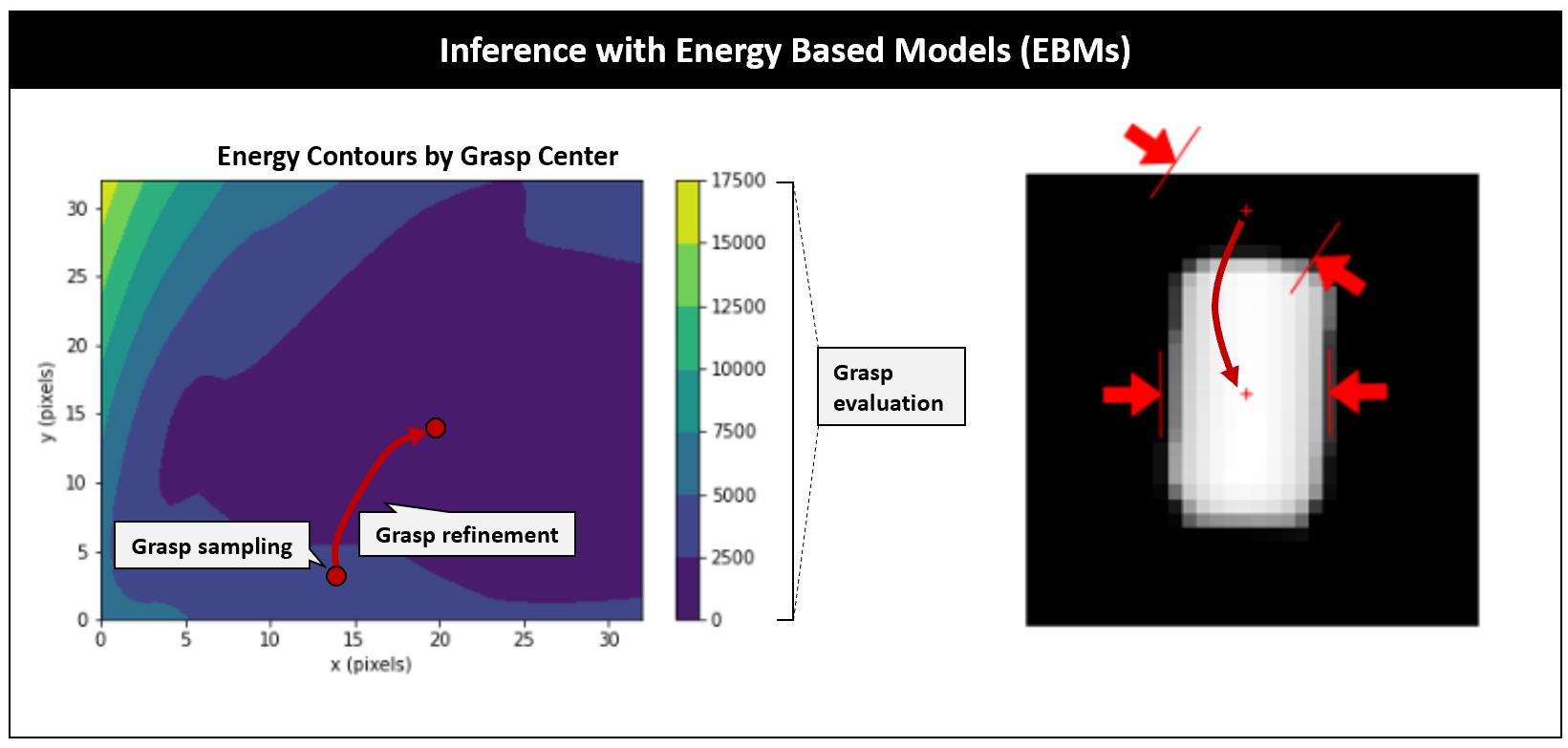
ebm-inference — Figure 2: EBMs unify grasp sampling, evaluation, and refinement by descending the energy manifold.

Experiment Setup

A subset of 220,000 examples from the DexNet 2.0 dataset was used for training and validation. DexNet 2.0 contains 6.7 million synthetic depth images and grasps generated from 1,500 3D object models. Each grasp is represented by a 4D vector: center row, center column, depth, and binary success label.

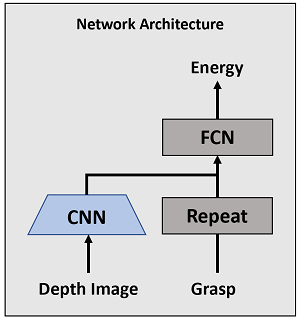
The network consists of a convolutional encoder for depth features and a fully connected energy head. The grasp vector is repeated and concatenated with visual features before entering the MLP, which outputs a scalar energy.

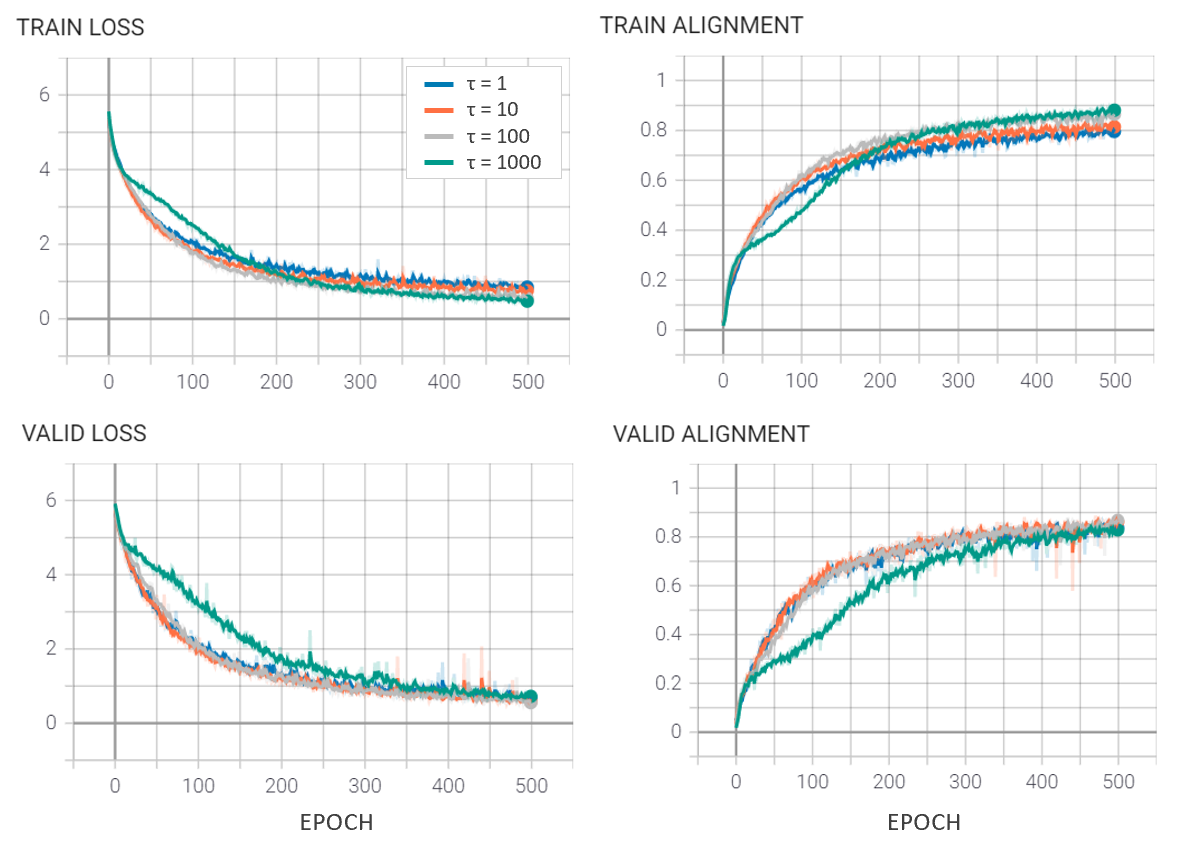
The model was trained with batch size 512, learning rate 1e-4, and temperature (\tau \in {1, 10, 100, 1000}). An alignment metric was monitored — the percentage of positive samples with energy lower than any negative sample in the batch.

Results

Training for 500 epochs across temperature values revealed that (\tau = 100) achieved the best alignment (86.8%). Higher temperatures improve stability by widening the energy separation between positives and negatives.

training-curves — Figure 5: Training curves across temperature values.

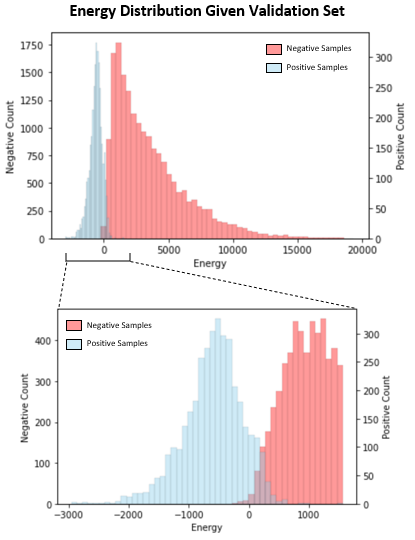
energy-distribution — Figure 6: Validation energy distributions show separation between successful (low-energy) and failed (high-energy) grasps.

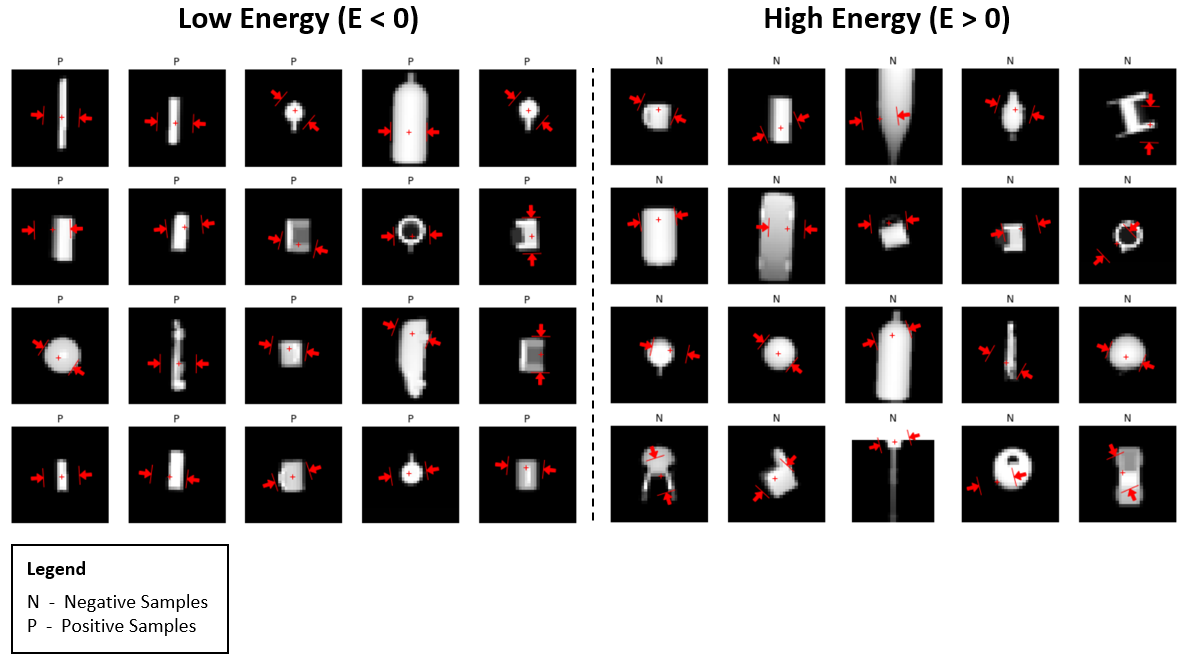
high-vs-low-energy — Figure 7: Visual comparison of low-energy (successful) and high-energy (failed) grasp samples.

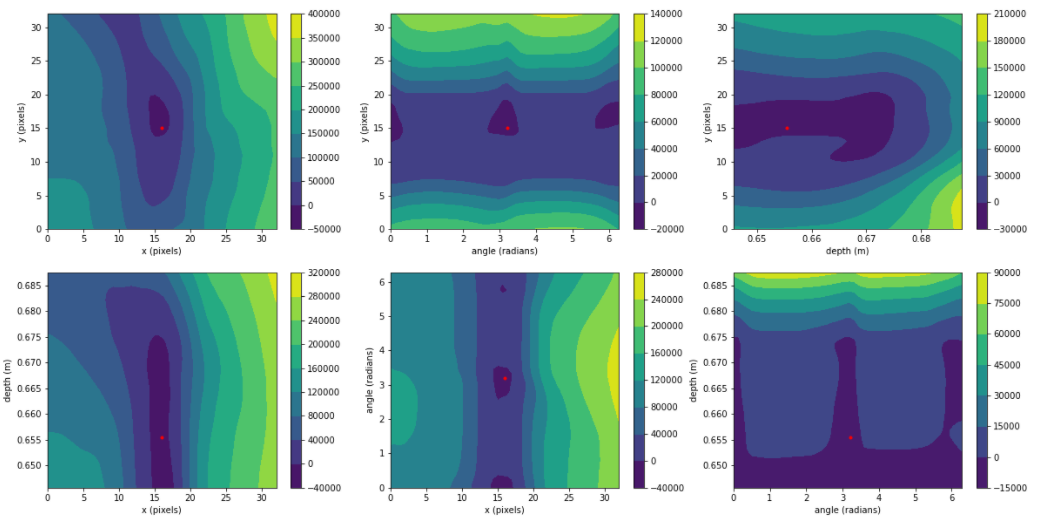
The energy contours (Figures 8–9) illustrate local minima around successful grasps, confirming that the EBM learns a smooth manifold corresponding to grasp quality.

inference-example — Figure 8: Example depth image and grasp pair used for inference visualization.

Grasp Generation in Action

The video below shows examples of grasps refined by gradient descent over the learned energy manifold. Starting from random initializations, the grasps converge to valid configurations.

Conclusion

Energy-based models offer a powerful unifying framework for grasp planning. By embedding sampling, evaluation, and refinement into a single differentiable process, the EBM bridges the gap between current two-stage approaches. The trained model generalizes to unseen objects, differentiates grasp quality, and generates physically plausible grasps via energy descent.

Future work includes deploying this model in full 3D simulation and coupling it with a learned grasp success predictor for closed-loop control.

References

Mahler, J. et al., “Dex-Net 2.0: Deep Learning to Plan Robust Grasps with Synthetic Point Clouds and Analytic Grasp Metrics.” RSS, 2017.
Mousavian, A., Eppner, C., and Fox, D., “6-DOF GraspNet: Variational Grasp Generation for Object Manipulation.” ICCV, 2019.
Murali, A. et al., “6-DOF Grasping for Target-driven Object Manipulation in Clutter.” ICRA, 2020.
LeCun, Y. et al., “A Tutorial on Energy-based Learning.” MIT Press, 2007.
Gutmann, M. and Hyvӓrinen, A., “Noise-contrastive estimation: A new estimation principle for unnormalized statistical models.” AISTATS, 2010.
Misra, I. and van der Maaten, L., “Self-supervised learning of pretext-invariant representations.” arXiv:1912.01991, 2019.
Chen, T., Kornblith, S., Norouzi, M., and Hinton, G., “A Simple Framework for Contrastive Learning of Visual Representation.” ICML, 2020.